Quantum Chemistry

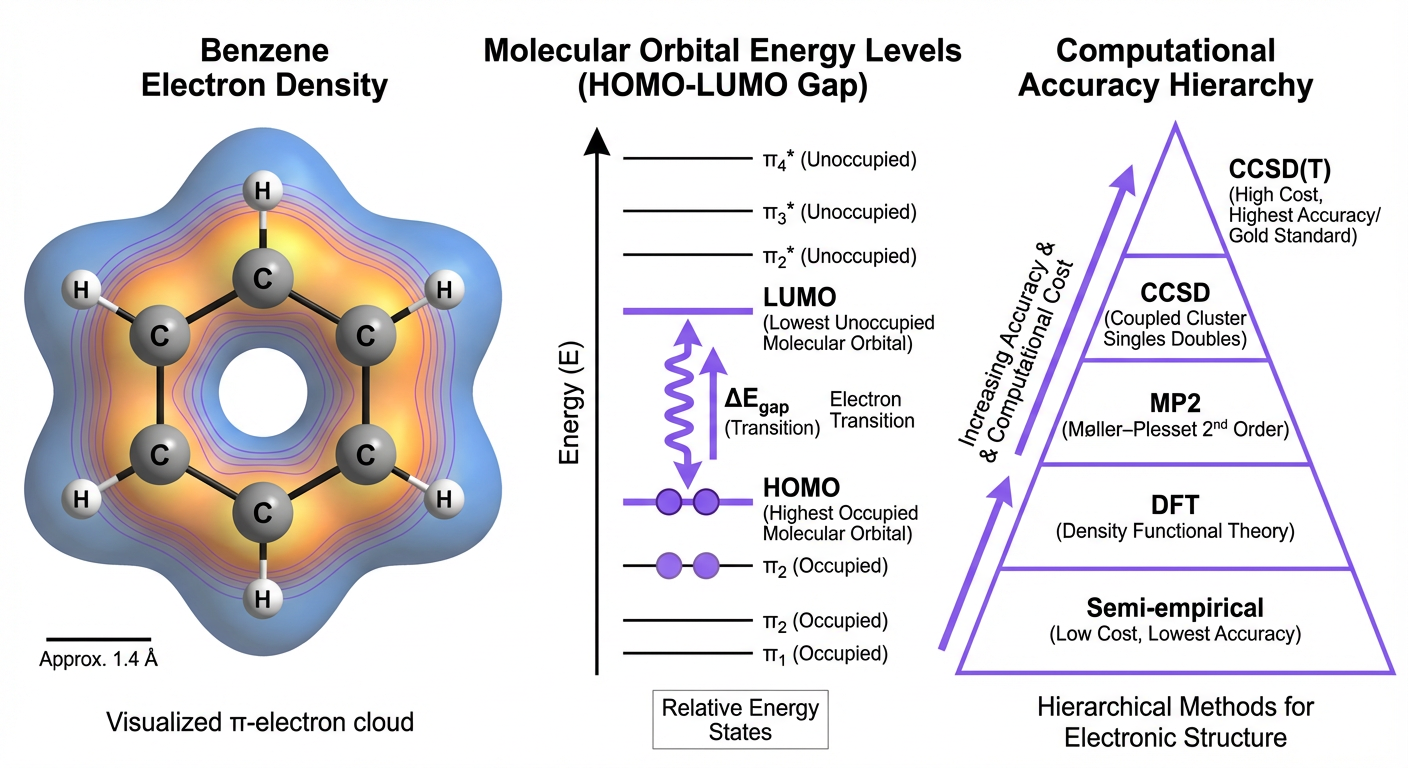
My research program is built on a foundation of quantum chemistry and electronic structure theory, which provides both the methodological rigor and the reference data essential for developing transferable machine learning potentials. Understanding the trade-offs between accuracy and computational cost across different levels of theory—from semi-empirical methods through density functional approximations to coupled-cluster approaches—directly informs how we design ML models, select training data, and interpret predictions in chemically relevant contexts.

Electronic Structure Foundations

Quantum chemistry provides exact solutions for simple systems and systematically improvable approximations for complex molecules. My early work explored these methods extensively, applying density functional theory (DFT) and ab initio approaches to problems in thermochemistry, reaction mechanisms, and molecular structure prediction. This background established critical insights: semi-empirical methods offer speed but limited transferability; standard DFT functionals struggle with dispersion interactions and charge-transfer states; post-Hartree-Fock methods provide systematic accuracy but scale unfavorably with system size.

These limitations motivated my transition toward machine learning as a means to extend quantum-level accuracy to larger and more complex chemical systems. However, the lessons from quantum chemistry remain central to my current research. The choice of reference method for training data—whether B3LYP, range-separated functionals like wB97X, or coupled-cluster CCSD(T)—directly affects the quality ceiling of any downstream ML model. Similarly, understanding when DFT approximations break down (strongly correlated systems, radical species, transition metals) helps identify regimes where ML potentials require particular care or additional validation.

Density Functional Theory Applications

Density functional theory remains the workhorse of computational chemistry, and my research has applied DFT across diverse chemical problems. Applications have included structure-property relationships for energetic materials and nitroaromatic compounds, thermochemistry of intermolecular complexes with benchmark accuracy requirements, electronic structure and bonding in organometallic systems, and reaction mechanism elucidation for organic transformations.

A recurring theme in this work is the importance of selecting appropriate functionals and basis sets for the problem at hand. Range-separated hybrid functionals prove essential for charge-transfer states; dispersion corrections are mandatory for non-covalent interactions; relativistic effects must be considered for heavy-element systems. These considerations now inform how we construct training datasets for machine learning potentials, ensuring that reference calculations capture the relevant physics across the intended application domain.

Ab Initio Molecular Dynamics

Car-Parrinello molecular dynamics (CPMD) and related ab initio molecular dynamics methods bridge quantum chemistry and statistical mechanics, enabling the study of molecular motion on quantum-derived potential energy surfaces. My work has applied these methods to investigate the dynamical flexibility of nucleic acid bases under thermal fluctuations, hydration effects on biomolecular structure and dynamics, thermal decomposition pathways in energetic materials, and conformational sampling in systems where classical force fields prove inadequate.

These studies highlighted both the power and the limitations of ab initio molecular dynamics: the accuracy is compelling, but the computational cost restricts accessible timescales and system sizes. This gap—accurate but expensive versus fast but approximate—represents the core motivation for developing machine learning potentials that can approach quantum accuracy at classical cost.

Coupled-Cluster and High-Accuracy Methods

For problems requiring benchmark accuracy, coupled-cluster methods—particularly CCSD(T)—provide the gold standard. My research has employed these methods for developing reference datasets for ML potential training, establishing thermochemical benchmarks for method validation, understanding the limitations of more approximate methods, and calibrating uncertainty estimates for computational predictions.

The AIQM (Artificial Intelligence Quantum Mechanical) series methods represent a synthesis of quantum chemistry and machine learning, using delta-learning to approach coupled-cluster accuracy at semi-empirical cost. AIQM3 extends this framework to seven main-group elements (H, C, N, O, S, F, Cl), targeting CCSD(T)-level accuracy while maintaining computational efficiency competitive with traditional semi-empirical methods. This work demonstrates that quantum chemistry expertise—understanding systematic errors, basis set effects, and the hierarchy of approximations—is essential for designing effective ML/QM hybrid approaches.

Reference Data for Machine Learning

The quality of machine learning potentials depends critically on the quality of reference quantum chemical calculations. My research addresses this connection through several strategies. Diverse configurational sampling ensures training sets cover the relevant regions of chemical space, including reactive configurations, strained geometries, and electronically complex states. Appropriate level of theory selection balances accuracy requirements against data generation costs, with range-separated DFT functionals often providing optimal trade-offs. Active learning protocols identify configurations where model uncertainty is high and additional quantum chemical calculations would be most informative. Benchmark validation against high-level calculations ensures that DFT-trained models remain reliable for properties of interest.

This work has generated training sets comprising millions of quantum chemical calculations—DFT optimizations, single-point energies, force calculations, and property predictions—that underpin the AIMNet family of transferable neural network potentials.

Outlook

Quantum chemistry remains central to my research program, both as a source of physical insight and as the foundation for reference data generation. Future directions include extending ML/QM hybrid methods to electronically complex systems including open-shell species and transition metals, developing active learning protocols that efficiently explore chemical space while minimizing expensive high-level calculations, understanding and quantifying the systematic errors introduced by using DFT reference data for ML training, and advancing toward “chemical intelligence” systems where quantum chemical calculations are deployed adaptively based on uncertainty estimates. The long-term vision is not to replace quantum chemistry with machine learning, but to extend its reach—making high-accuracy atomistic modeling routine for complex chemical problems that would otherwise be computationally intractable.